元利均等返済と元金均等返済の違いは、元金と元利金のどちらかを均等に設定して返済額を求めているかの違いです。
「元金とは?」「元利金ってなに?」と思った方のために、元利均等返済と元金均等返済の違いや、メリット・デメリット、どっちがお得で誰に向いているのかについて、わかりやすく解説します。
- 元金とは?元利金とは?
- 元利均等返済と元金均等返済の違い
- どっちがお得?
- 2つの返済方法のメリット・デメリット
- 元金均等返済に向いている人は、こんな方
- 元利均等返済に向いている人は、こんな方
元金と元利金
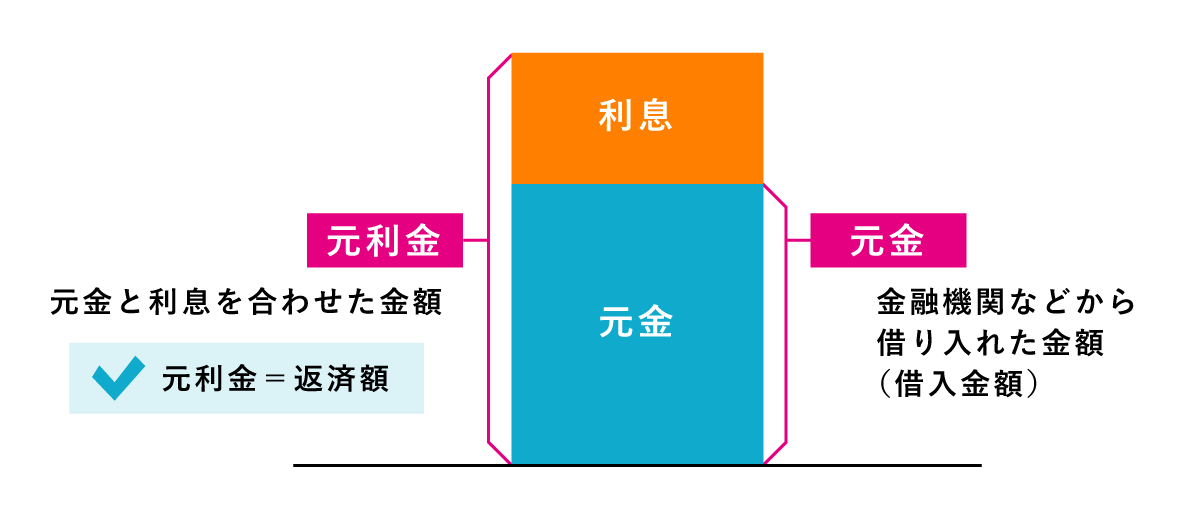
元利均等返済と元金均等返済の違いを理解するには、「元金」と「元利金」がどのようなものなのか知ることが近道です。
元金とは?
住宅ローンの元金とは 『土地や住宅を購入するために金融機関などから借り入れた金額』のことです。
例えば、頭金なしで3,980万円の建売住宅を購入する場合は、金融機関から3,980万円を借り入れることになるため、元金は3,980万円になります。
頭金400万円で3,980万円の建売住宅を購入する場合は、
を金融機関から借り入れるため、元金は3,580万円となります。
元利金とは?
住宅ローンの元利金とは 『金融機関などから借り入れた金額と利息を合わせた金額』のことです。
金融機関などから借り入れた金額は、「元金」のことですので、
の計算で求められます。
住宅ローンを借りる場合は、元金を返せばいいというわけではなく、借りている間の対価として「利息」を支払わなければいけません。
つまり、元利金とは、住宅ローンの返済額そのものです。
元利均等返済と元金均等返済の違いは?
住宅ローンの返済方法は、「元利均等返済」と「元金均等返済」の2つがあります。
- 元利均等返済
- 元金均等返済
元利均等返済と元金均等返済の違いは、「元金と元利金のどちらかを均等に設定して返済額を求めているか」の違いでした。
元利均等返済方式

元利均等返済とは 『元金分と利息分を合わせた金額(返済額)が毎月一定となる返済方法』のことです。
元金分と利息分を合わせた金額は、「元利金」のことですので、元利金が毎月一定となる返済方法ということになります。
ちなみに、元利均等返済の読み方は、「がんりきんとうへんさい」と言います。
なお、一般的には変動金利は5年ごとに見直されますので、毎月返済額は変わりますが、5年間の毎月返済額は一定になります。
元金均等返済方式
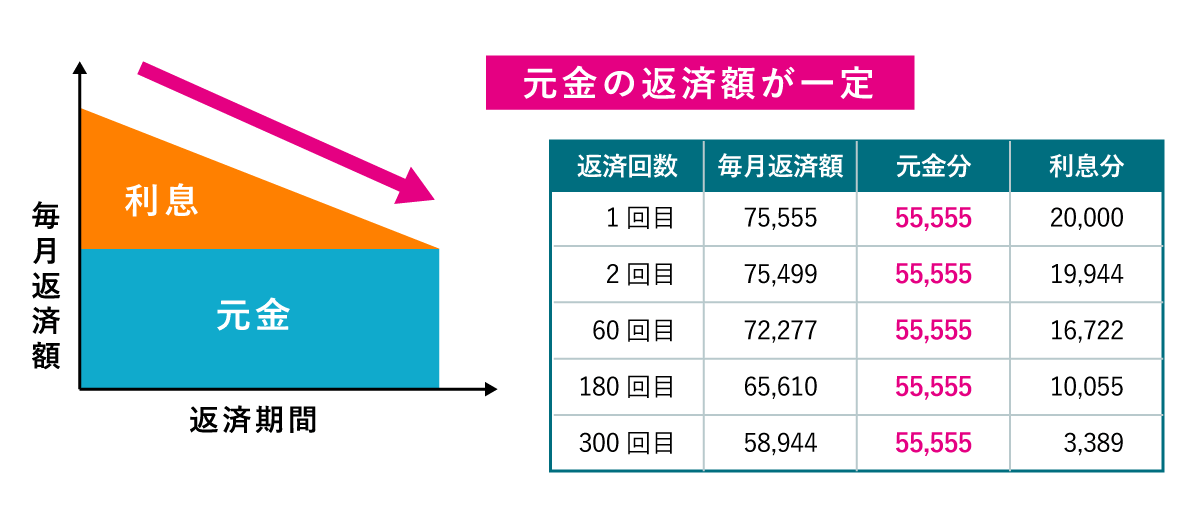
元金均等返済とは 『元金分を毎月均等にして、利息と合わせて返済する方法』のことです。
元金均等返済の読み方は、「がんきんきんとうへんさい」と言います。
元金均等返済は、読んで字の如く、元金を均等にして返済する方法と覚えやすいですが、元利均等返済がどのようなものだったか忘れそうな場合は、以下のように覚えておくとよいでしょう。
元利均等返済と元金均等返済は、どっちがお得?
元利均等返済と元金均等返済の、どっちがお得かについて、先に結論をいうと、元金均等返済の方がお得です。
以下は、同じ条件で計算した元利均等返済と元金均等返済の総返済額シミュレーションデータです。
| 条件 [借入金額、金利(固定金利)、返済期間] |
元利均等返済 の総返済額[A] |
元金均等返済 の総返済額[B] |
差額 [A]-[B] |
|---|---|---|---|
| 3,000万円、1.0%、20年 | 33,112,271円 | 33,012,400円 | 99,871円 |
| 3,000万円、1.0%、35年 | 35,567,804円 | 35,262,332円 | 305,472円 |
| 5,000万円、1.0%、20年 | 55,187,192円 | 55,020,722円 | 166,470円 |
| 5,000万円、1.0%、35年 | 59,279,814円 | 58,770,669円 | 509,145円 |
| 3,000万円、1.5%、20年 | 34,743,155円 | 34,518,660円 | 224,495円 |
| 3,000万円、1.5%、35年 | 38,579,007円 | 37,893,605円 | 685,402円 |
| 3,000万円、2.0%、20年 | 36,423,456円 | 36,024,920円 | 398,536円 |
| 3,000万円、2.0%、35年 | 41,738,968円 | 40,524,873円 | 1,214,095円 |
総返済額シミュレーションデータを見ると、全ての条件において、元金均等返済の総返済額が安いです。
なら、元金均等返済を選べばいいかといえば、そうとも言い切れません。
こちらは、上記シミュレーションデータと同じ条件の1回目返済額のデータになります。
| 条件 [借入金額、金利(固定金利)、返済期間] |
元利均等返済 の1回目返済額[A] |
元金均等返済 の1回目返済額[B] |
差額 [A]-[B] |
|---|---|---|---|
| 3,000万円、1.0%、20年 | 137,968円 | 150,000円 | -12,032円 |
| 3,000万円、1.0%、35年 | 84,685円 | 96,428円 | -11,743円 |
| 5,000万円、1.0%、20年 | 229,947円 | 249,999円 | -20,052円 |
| 5,000万円、1.0%、35年 | 141,142円 | 160,713円 | -19,571円 |
| 3,000万円、1.5%、20年 | 144,763円 | 162,500円 | -17,737円 |
| 3,000万円、1.5%、35年 | 91,855円 | 108,928円 | -17,073円 |
| 3,000万円、2.0%、20年 | 151,765円 | 175,000円 | -23,235円 |
| 3,000万円、2.0%、35年 | 99,378円 | 121,428円 | -22,050円 |
1回目返済額シミュレーションデータを見ると、全ての条件において、元利均等返済の1回目返済額が安いことが分かります。
元金均等返済の1回目返済額でも十分返せるのであれば、元金均等返済の方が断然安く付くため、元金均等返済を選択しても問題ありませんが、「支払いが厳しいかも」と思った方は、じっくりシミュレーションして検討されたほうがよいです。
住宅ローン返済方法のメリット・デメリット
元利均等返済と元金均等返済のどっちがいいか、まだ悩まれている方は、それぞれのメリット・デメリットを確認しましょう。
| 元利均等返済方式 | 元金均等返済方式 | |
|---|---|---|
| 返済イメージ | 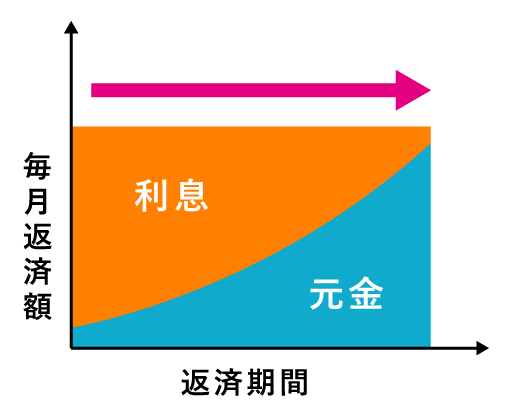 |
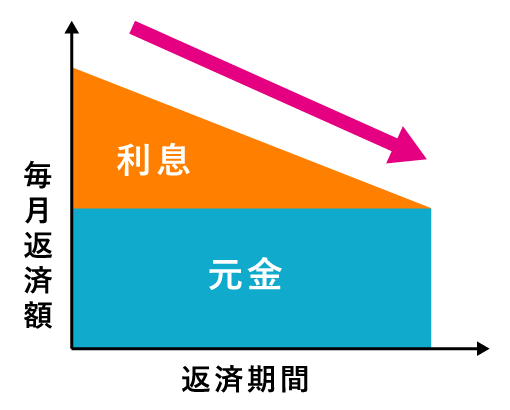 |
| メリット | ・毎月返済額が一定で、返済計画が立てやすい ・返済開始当初は、元金均等返済より返済額が少ない |
・返済が進むにつれて、毎月返済額が少なくなる ・同条件で、元利均等返済より総返済額が少ない |
| デメリット | ・同条件で、元金均等返済より総返済額が多い ・元金の減り方が遅く、利息が高い |
・返済開始当初の返済額が多い ・借入可能額が少なくなる |
元利均等返済と元金均等返済のメリット・デメリットは、双方が反比例の関係にあります。
基本的に、お金に関する内容が多いですが、この中で押さえておくポイントは以下の2つです。
- 【元利均等返済のメリット】毎月返済額が一定で、返済計画が立てやすい
- 【元金均等返済のデメリット】借入可能額が少なくなる
毎月返済額が一定で、返済計画が立てやすい
元利均等返済は、毎月の返済額が一定のため、返済計画が立てやすいことがメリットによく挙げられます。
しかし、家計の支出は、時期によって変化しますので、毎月の返済計画を立てる際には、元金均等返済で返済計画が立てにくいとは、あまり感じません。
子供の教育費など将来の家計の支出を把握して、無理な返済時期がないかをしっかり見極めましょう。
借入可能額が少なくなる
元金均等返済のデメリットに挙げた「借入可能額が少なくなる」については、購入あるいは建築予定の住宅費用を、借りられるかがポイントです。
住宅ローンのシミュレーションをする場合は、借入金額から毎月返済額を求めて、毎月支払えるか確認する方法や、可能な毎月返済額からどれぐらい借りられるのかを確認する方法など、いろいろな角度からシミュレーションします。
もしも、可能な毎月返済額から元金均等返済を選択すると借入金額が少なく、住宅費用を用意できない場合もあります。
こちらは、1回目返済額が同じ場合の、借入可能額シミュレーションデータです。
| 条件 [1回目返済額、金利(固定金利)、返済期間] |
元利均等返済 の借入可能額[A] |
元金均等返済 の借入可能額[B] |
差額 [A]-[B] |
|---|---|---|---|
| 8万円、1.0%、20年 | 1,740万円 | 1,600万円 | 140万円 |
| 8万円、1.0%、35年 | 2,834万円 | 2,489万円 | 345万円 |
| 10万円、1.0%、20年 | 2,175万円 | 2,000万円 | 175万円 |
| 10万円、1.0%、35年 | 3,543万円 | 3,111万円 | 432万円 |
| 8万円、1.5%、20年 | 1,658万円 | 1,477万円 | 181万円 |
| 10万円、1.5%、35年 | 3,266万円 | 2,754万円 | 512万円 |
| 8万円、2.0%、20年 | 1,581万円 | 1,371万円 | 210万円 |
| 10万円、2.0%、35年 | 3,019万円 | 2,471万円 | 548万円 |
借入可能額を比較すると100万円単位の差があります。
100万円単位のお金は、簡単に用意できる金額ではないため、毎月返済額から元金均等返済を選択すると、住宅費用が足りなくなる恐れがありますので、注意しましょう。
結局どっちの返済方法がいい!?
元利均等返済と元金均等返済のどちらかを選ぶには、返済額の比較だけでなく、将来のライフスタイルの変化も考慮すると失敗しません。
金額だけであれば、元金均等返済が断然お得なので、まずは、元金均等返済でライフスタイルの変化を考慮した返済計画を立てましょう。
もしも、厳しそうであれば、元利均等返済で返済計画を立てるか、頭金を親族から借りるなど検討しましょう。
元金均等返済が向いている人
元金均等返済が向いている人は、こんな方たちです。
- 希望の借入額で、毎月返済額が家計を圧迫しない人
- 現在、返済に余裕があって、将来、支出増(収入減)の見込みのある人
希望の借入額で、毎月返済額が家計を圧迫しない人
こちらは、要はお金に余裕がある方です。
元金均等返済の一番のネックは、返済開始当初の返済額が多いことですので、そこをクリアできるだけの資金がある方は、元金均等返済がオススメです。
現在、返済に余裕があって、将来、支出増(収入減)の見込みのある人
こちらは、小さな子供がいる世帯や、共働き世帯の方が当てはまります。
子供がいる世帯で、支出が増える要因は、もちろん学費です。
学費は、「公立・私立」と「どこまで進学するか」で、大きく変ってきます。
学費の支出が増えれば、住宅ローンが負担になるため、あまり学費がかからないうちに、返済額を減らしたい方は、元金均等返済がオススメです。
他にも、共働きで将来子供がほしい方は、育児のためにどちらかが、仕事をやめることも想定されます。
そうなると、世帯収入が減りますので、将来、住宅ローンが負担になる可能性があるので、余裕があるうちに、返済額を減らしたほうが、無理がありません。
どちらも基本的には、余裕のある時期に先に返済して、支出増(収入減)の時期に負担にならないように考えているに向いている返済方法です。
元利均等返済が向いている人
元金均等返済が向いている人は、こんな方たちです。
- 元金均等返済では、希望する金額を借りられない人
- なるべく毎月の返済額を減らしたい人
元金均等返済では、希望する金額を借りられない人
こちらは、住宅ローンにまわすお金が少なく、希望する金額を借りられない方です。
毎月の可能な返済額と元金均等返済でシミュレーションしてみて、借入可能額では住宅購入に足りない場合は、元利均等返済で返済計画を立てましょう。
ここでのポイントは、収入ではなく、毎月の可能な返済額です。
収入が多くても、支出するものが多ければ、収入が少ない方よりも毎月の可能な返済額が少ないケースもあります。
毎月の可能な返済額を、しっかり把握しましょう。
なるべく毎月の返済額を減らしたい人
こちらは、手元になるべくお金を残しておきたい方です。
お金に余裕があっても、将来何かあったときのために、手元にお金を残しておきたい方は、元利均等返済がオススメです。
総返済額が増えても、手元にお金を残しておきたいと考える方は多いですが、繰り上げ返済をすれば元利均等返済でも総返済額を少なくできる可能性もあります。
こちらに該当する方は、繰り上げ返済も考慮して返済計画を立てると失敗がありません。
まとめ
ここまで、元利均等返済と元金均等返済の違いや、メリット・デメリット、どっちがお得で誰に向いているのかについて、分かりやすく解説しました。
住宅ローンの返済額は、返済方法だけでなく、固定金利・変動金利でも変ってきます。
シミュレーションする場合も、毎月返済額→借入可能額、借入金額→毎月返済額、年収→借入可能額と、いろいろな角度からシミュレーションができます。
住宅ローンは、主に「金利」「返済期間」「返済方法」の3つで決まりますので、いろいろ検討してみましょう。
住宅ローン返済額・借入可能額を求める方法

すべて無料!住宅ローン計算アプリ厳選3選!
- 簡単操作でサクっと返済額を求めたい人向けアプリ
- 大まかな返済額と比較ができればいい人向けアプリ
- 繰り上げ返済をパターン別に比較した人向けアプリ

電卓を使った住宅ローンの計算方法!元利均等返済と元金均等返済に対応!
- 元利均等返済と元金均等返済の違い
- 住宅ローン返済額の計算式
- 電卓を使った簡単な計算方法
- 【おまけ】電卓が無くてもGoogle電卓で簡単に計算する方法
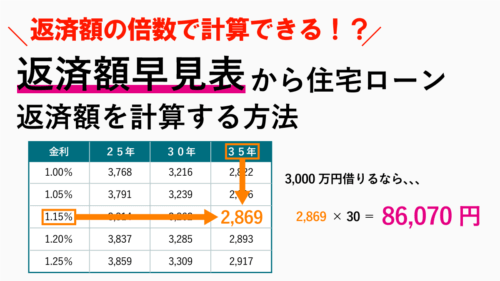
住宅ローン返済額早見表!100万円当たりの返済額の倍数で簡単計算!
- 元利均等返済と元金均等返済の違い
- 返済額早見表の計算式と注意点
- 元利均等返済の返済額早見表(毎月返済額)
- 元金均等返済の返済額早見表(1回目返済額)

【無料】元利均等返済と元金均等返済に対応したエクセルテンプレート
- テンプレートのダウンロード
- テンプレートの使い方
- シミュレーション結果の比較と計算根拠
- その他のシミュレーション方法