住宅ローンの金利を計算するには、「金利と利息の関係」「単利と複利の仕組み」が分かると、どれぐらい利子が増えて、返済額がいくらになるのかイメージしやすいです。
今回は、金利と利息の関係や単利と複利の仕組みから、住宅ローン金利の計算方法について、分かりやすく解説します。
- 金利と利息の関係
- 単利と複利の仕組み
- 住宅ローンの金利タイプと返済方法
- 住宅ローン金利の計算方法
金利と利息の関係

金利とは 『お金を借りた際に利息を計算する元になる利率』で、利息とは 『お金を貸した対価として、一定の割合で支払われるお金』のことです。
利息は利子とも呼ばれますが、一般的に以下のように説明されることが多いです。
- 借りたときに支払うものは利子→住宅ローンの利子を払う
- 貸したときに受け取るものは利息→住宅ローンの利息を受け取る
ただ、厳密に使い分けられているわけではないですが、住宅ローンでは上記のように解釈しても問題ありません。
金利と利息の計算式
金利と利息の関係を計算式で表すと、以下のようになります。
例えば、「借入期間が1年」「金利が年1%」で100万円を借りたときの利息は、
となります。
返済額の計算式は
となりますので、
を返済しなければいけません。
ただし、住宅ローンの場合は、このような単純な計算方法ではありません。
単利と複利の仕組み
利息の計算方法には、以下の2つがあります。
- 単利
- 複利
単利
単利とは 『元金に対してのみ利息を計算する方式』のことです。
単利は、現金にのみ利息が発生しますので、単利の計算式は、以下のようになります。
例えば、「借入期間が1年」「金利が年1%」で100万円を借りたときの総返済額は、
で、「借入期間が5年」「金利が年1%」で100万円を借りたときの総返済額は、
となります。
複利
複利とは 『利息を元金に繰り入れて、利息を計算する方式』のことです。
単純な複利計算を例にあげると、1年目の利息は、
と単利と変わりませんが、2年目の利息は、元金に1年目の利息を繰り入れて、計算されます。
この複利を計算式で表すと、以下のようになります。
例えば、「貸借期間が5年」「金利が年1%」で100万円を借りたときの総返済額は、
となります。
| 返済期間 | 単利の 総返済額[A] |
複利の 総返済額[B] |
差額 [B]-[A] |
|---|---|---|---|
| 5年 | 1,060,000円 | 1,061,457円 | 1,457円 |
| 10年 | 1,120,000円 | 1,126,692円 | 6,692円 |
| 15年 | 1,180,000円 | 1,195,935円 | 15,935円 |
| 20年 | 1,240,000円 | 1,269,434円 | 29,434円 |
| 25年 | 1,300,000円 | 1,347,450円 | 47,450円 |
| 30年 | 1,360,000円 | 1,430,261円 | 70,261円 |
| 35年 | 1,420,000円 | 1,518,161円 | 98,161円 |
こちらは、「元金が100万円」「金利が年1.2%」で、返済期間別の総返済額をシミュレーションしたデータです。
よく複利は、「利息が利息を生む」と言いますが、借入期間が長ければ長いほど、利息が増えているのがわかります。
住宅ローンは「複利計算」
住宅ローンは、この「複利計算」で計算されます。
つまり、住宅ローンの返済額は、借入期間が長くなるほど、利息の増え方が大きくなるため、借入期間を短くすることが利息負担を少なくすることに繋がります。
ただし、借入期間を短くすると毎月の返済額が増えるため、家計を圧迫する可能性もあります。
返済計画を立てるときは、「住宅ローンは、借入期間が長くなるほど利息が大きく増える」ことを理解しながら、無理のない返済計画を立てましょう。
住宅ローンの金利タイプ
金利と利息の関係は理解できたと思いますが、住宅ローンの金利タイプには、大きく分けて以下の2つがあります。
- 固定金利
- 変動金利
固定金利
固定金利とは 『借り入れ時の金利が全借り入れ期間を通じて変わらない金利』のことです。
将来にわたって、市場金利が上がっても下がっても借入金利は変わらないため、毎月の返済額は固定で住宅ローンの返済計画が立てやすいのがメリットです。
ただし、市場金利が低下した場合も返済額が変わらないため、市場よりも返済額が多くなります。
メリット
- 金利が固定で、安心感がある
- 返済額が変わらないので住宅ローンの返済計画が立てやすい
デメリット
- 市場金利が下がると変動金利よりも返済額が多くなる
- 変動金利よりも金利が高い
変動金利
変動金利とは 『金融情勢により定期的に借入金利が見直される金利』のことです。
市場金利が下がると金利も変動し、返済額が少なくなるメリットがありますが、市場金利が上がると返済額が大きくなります。
金利が変動するため、住宅ローンの返済計画が立てにくいのがデメリットの1つです。
一見、変動金利は不安定のように見えますが、住宅ローンの金利タイプの中で一番金利が低く設定されているのが、変動金利です。
メリット
- 金利が下がると、返済額が少なくなる
- 固定金利よりも金利が低い
デメリット
- 市場金利が上がるリスクがある
- 市場金利の変動により住宅ローンの返済計画が立てにくい
住宅ローンの返済方法
住宅ローンの返済方法には、大きく分けて以下の2つがあります。
- 元利均等返済
- 元金均等返済
元利均等返済

元利均等返済とは 『元金分と利息分を合わせた返済額が毎月一定となる返済方法』のことです。
元利均等返済は、毎月の返済額が一定のため、住宅ローンの返済計画が立てやすいメリットがあります。
他にも、返済当初の返済額が元金均等返済よりも少ないのもメリットの1つです。
返済期間が少なくなるほど、元金均等返済の方が返済額が少なくなりますが、返済当初は引越し代などまとめて費用がかかるので、負担の少ない元利均等返済を選ぶ方も多いです。
メリット
- 返済額が一定のため、住宅ローンの返済計画が立てやすい
- 返済当初の返済額が元金均等返済よりも少なくすることができる
デメリット
- 借入金残高の減り方が遅くなる
- 同じ借入期間の場合、元金均等返済よりも総返済額が多くなる
| 返済回数 | 毎月返済額(円) | 毎月返済額の 元金分(円) |
毎月返済額の 利息分(円) |
住宅ローン 残高(円) |
|---|---|---|---|---|
| 1回目 | 66,181 | 46,181 | 20,000 | 19,953,819 |
| 2回目 | 66,181 | 46,228 | 19,953 | 19,907,591 |
| 3回目 | 66,181 | 46,274 | 19,907 | 19,861,317 |
| 60回目 (5年後) |
66,181 | 48,987 | 17,194 | 17,145,767 |
| 120回目 (10年後) |
66,181 | 52,014 | 14,167 | 14,115,130 |
| 180回目 (15年後) |
66,181 | 55,229 | 10,952 | 10,897,179 |
| 240回目 (20年後) |
66,181 | 58,643 | 7,538 | 7,480,350 |
| 300回目 (25年後) |
66,181 | 62,267 | 3,914 | 3,852,342 |
| 359回目 | 66,181 | 66,049 | 132 | 66,226 |
| 360回目 | 66,292 | 66,226 | 66 | 0 |
| 合計 | 23,825,271 | 20,000,000 | 3,825,271 | – |
こちらは、以下の条件で金利計算した返済額のシミュレーションデータです。
- 借入金額:2,000万円
- 金利:年1.2%
- 返済期間:30年
- 金利タイプ:固定金利
- 返済方法:元利均等返済
返済額のシミュレーションデータを見ると、毎月返済額が「66,181円」と毎月一定となります。
実際には、1回目は日割りで計算され、最後の月も若干の返済額の差が生じます。
元金均等返済
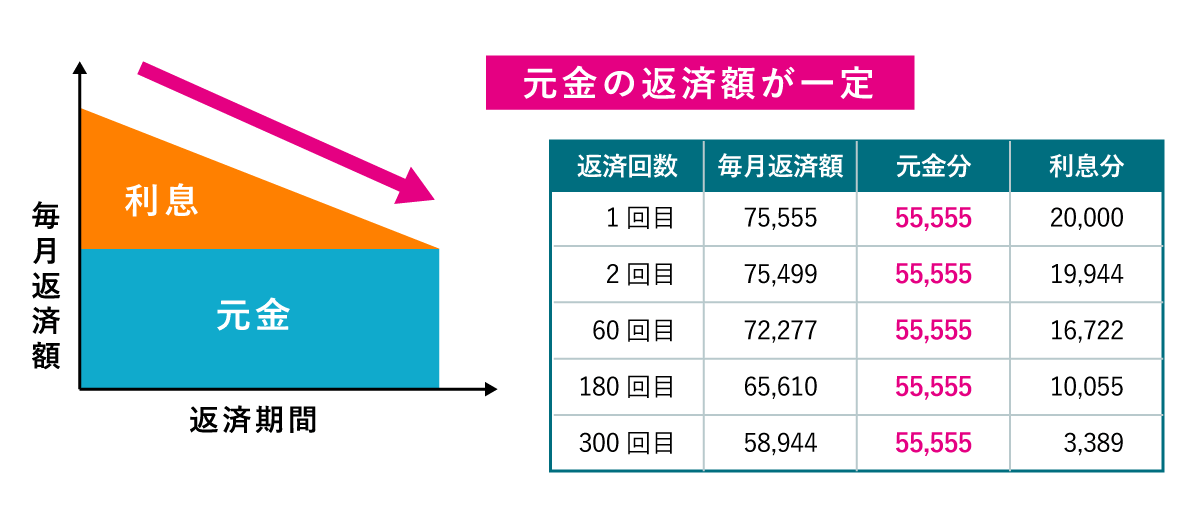
元金均等返済とは 『元金分を毎月均等に返済し、利息を含めて返済する方法』のことです。
元金均等返済は、元金分を毎月均等に返済するため、返済当初の返済額が高くなりますが、元利均等返済よりも元金返済のペースが速いので、返済が進むと返済額が少なくなっていきます。
メリット
- 返済が進むと返済額が少なくなっていく
- 同じ借入期間の場合、元金均等返済よりも総返済額が少なく済む
デメリット
- 返済当初の返済額が高い
| 返済回数 | 毎月返済額(円) | 毎月返済額の 元金分(円) |
毎月返済額の 利息分(円) |
住宅ローン 残高(円) |
|---|---|---|---|---|
| 1回目 | 75,555 | 55,555 | 20,000 | 19,944,445 |
| 2回目 | 75,499 | 55,555 | 19,944 | 19,888,890 |
| 3回目 | 75,443 | 55,555 | 19,888 | 19,833,335 |
| 60回目 (5年後) |
72,277 | 55,555 | 16,722 | 16,666,700 |
| 120回目 (10年後) |
68,943 | 55,555 | 13,388 | 13,333,400 |
| 180回目 (15年後) |
65,610 | 55,555 | 10,055 | 10,000,100 |
| 240回目 (20年後) |
62,277 | 55,555 | 6,722 | 6,666,800 |
| 300回目 (25年後) |
58,944 | 55,555 | 3,389 | 3,333,500 |
| 359回目 | 55,666 | 55,555 | 111 | 55,755 |
| 360回目 | 55,810 | 55,555 | 55 | 0 |
| 合計 | 23,609,858 | 20,000,000 | 3,609,858 | – |
こちらは、以下の条件で金利計算した返済額のシミュレーションデータです。
- 借入金額:2,000万円
- 金利:年1.2%
- 返済期間:30年
- 金利タイプ:固定金利
- 返済方法:元金均等返済
元利均等返済は毎月の返済額が一定でしたが、元金均等返済は返済額の元金分が「55,555円」と毎月一定となっています。
返済額の総額を比較すると元利均等返済で「23,825,271円」、元金均等返済で「23,609,858円」となり
の差があります。
このように元利均等返済は、元金均等返済よりも返済総額が高いのが特徴です。
住宅ローン金利の計算方法
住宅ローン金利の計算方法は複雑で、同じ借入金額や返済期間でも条件によって毎月の返済額や総返済額が大きく変わってきます。
住宅ローンの計算には、いくつかの方法がありますが、最初に元利均等返済での住宅ローンの計算方法を分かりやすく説明します。
こちらは、元利均等返済での住宅ローンの計算式です。
【月利=金利÷12】【n=返済回数】
月利とは
月利とは 『借入金額に対して月単位でかかる利息』 のことです。
住宅ローンの金利は年単位の年利で記載されていますので、月利に変換するには、12ヶ月で割ります。
例えば、金利1.2%の場合の月利は、
となります。
nの返済回数は 『毎月支払う回数』のことです。
例えば、返済期間30年の場合は、
が返済回数となります。
計算例
| 金利タイプ | 固定金利 | 借入金額 | 3,000万円 |
|---|---|---|---|
| 返済方法 | 元利均等返済 | 返済期間 | 25年 |
| 金利 | 1.2% | 返済回数 | 300回(25年×12ヶ月) |
こちらの条件で、住宅ローンの計算式を使って毎月の返済額を求めていきます。
住宅ローンの計算式に数値を当てはめるとこのようになります。
こちらを計算すると毎月の返済額は「115,798円」となります。
住宅ローンの計算式には、返済回数部分が「べき乗」になっているため、計算するのが難しいと感じる方も多いです。
概算の返済額でも簡単に求めたいとい方は「返済額早見表」を使えば、簡単に概算の返済額を計算することもできます。
返済額早見表を使った返済方法を知りたい方は【 住宅ローン返済額早見表!100万円当たりの返済額の倍数で簡単計算! 】で詳しく説明してますので、ご確認ください。
まとめ
ここまで、金利と利息の関係や単利と複利の仕組みから、住宅ローン金利の計算方法について、解説しました。
ある程度、不動産購入の予算を決めているのであれば、毎月どれぐらいの返済額になるのか確認してみましょう。
住宅ローン返済額・借入可能額を求める方法

すべて無料!住宅ローン計算アプリ厳選3選!
- 簡単操作でサクっと返済額を求めたい人向けアプリ
- 大まかな返済額と比較ができればいい人向けアプリ
- 繰り上げ返済をパターン別に比較した人向けアプリ

電卓を使った住宅ローンの計算方法!元利均等返済と元金均等返済に対応!
- 元利均等返済と元金均等返済の違い
- 住宅ローン返済額の計算式
- 電卓を使った簡単な計算方法
- 【おまけ】電卓が無くてもGoogle電卓で簡単に計算する方法
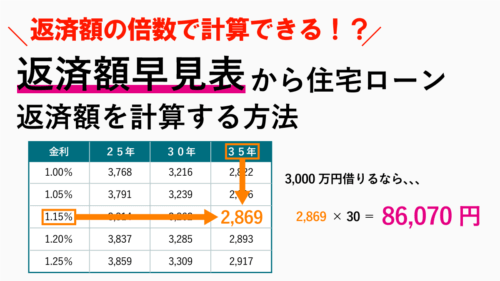
住宅ローン返済額早見表!100万円当たりの返済額の倍数で簡単計算!
- 元利均等返済と元金均等返済の違い
- 返済額早見表の計算式と注意点
- 元利均等返済の返済額早見表(毎月返済額)
- 元金均等返済の返済額早見表(1回目返済額)

【無料】元利均等返済と元金均等返済に対応したエクセルテンプレート
- テンプレートのダウンロード
- テンプレートの使い方
- シミュレーション結果の比較と計算根拠
- その他のシミュレーション方法
住宅ローンの基本の「き」

元利均等返済と元金均等返済の違いは?住宅ローン返済はどっちがお得?
- 元利均等返済と元金均等返済の違い
- 2つの返済方法のメリット・デメリット
- 元金均等返済に向いている人は、こんな方
- 元利均等返済に向いている人は、こんな方

